ПОЗИЦИОННЫЕ И НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления.

Система счисления – способ записи чисел с помощью цифр и правила действий со значениями этих цифр.

Системы счисления делятся на 2 группы: непозиционная и позиционная.

Непозиционная система счисления – система счисления, в которой значение цифры не зависит от её позиции в числе. (Римская система счисления)

Позиционная система счисления – система счисления, в которой значение цифры зависит от её позиции в числе.

Каждая позиционная система счисления имеет определенный алфавит цифр и основание.

Алфавит системы счисления – конечное и упорядоченное множество цифр, используемых для записи чисел в системе счисления.

Название любой позиционной системы счисления образуется от основания системы счисления.

Основание системы равно количеству цифр (знаков) в ее алфавите.

За основание позиционной системы счисления можно принимать любое натуральное число больше единицы. Если основание системы счисления больше десяти, то для записи цифр, значение которых равно десяти и более, используются буквы латинского алфавита

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом.

Представление чисел с помощью арабских цифр — самая распространённая позиционная система счисления, она называется «десятичной системой счисления». Десятичной системой она называется потому, что использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Для составления машинных кодов удобнее использовать двоичную систему счисления, содержащую только две цифры, 0 и 1. В двоичной системе максимальная цифра 1.

Правило построения последовательности целых положительных чисел в позиционных системах счисления:

1.      Для получения следующего целого числа надо в данном числе заменить саму правую цифру числа следующей по величине цифрой.

2.      Если какая – либо заменяемая цифра является самой старшей цифрой алфавита, то её надо заменить на 0, а цифру, стоящую слева от неё, заменить следующей по величине цифрой.

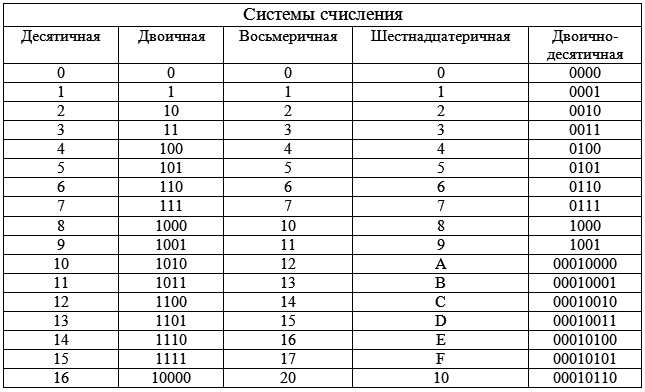
Таблица соответствия записи натуральных чисел в системах счисления:

Кодирование чисел разных позиционных систем счисления:

Записи чисел в системах счисления имеют две формы: свернутая и развернутая.

Свернутая форма – последовательность цифр.

Развернутая - сумма значений цифр.

Пример записи чисел из свернутой формы в развернутую:

Правило перевода целых чисел позиционных систем счисления в десятичную систему счисления:

1.      Пронумеровать разряды целого числа справа налево по возрастанию, начиная с нуля.

2.      Записать число в развернутой форме, заменив все цифры и основание системы счисления десятичными числами.

3.      Определить значение полученного выражения, выполнив арифметические действия в десятичной системе счисления.

Примеры: 

2357₈ = (2·8³)+(3·8²)+(5·8¹)+(7·8⁰) = 2·512 + 3·64 + 5·8 + 7·1 = 1263₁₀